On SPA Cross-Packet Ciphertext Entropy
13 February, 2012
 With fwknop now re-written in C for the 2.0 release,
I thought it would be a good idea to take a look at how close encrypted SPA packet data comes to having
high levels of entropy - as understood to be a measure of randomness - from one packet to the next. If
fwknop is properly using encryption, and the ciphers themselves are also well-implemented (fwknop can
use either Rijndael or GPG), then we would expect there to be no obvious relationship between SPA packets
even for repeated access requests to the same service. If there are any such relationships in the
encrypted data across multiple SPA packets, then an adversary might be able to infer things about
the underlying plaintext - precisely what strong encryption is supposed to make difficult. This blog
post covers SPA packet entropy for AES (Rijndael) CBC and ECB encryption modes, and leaves GPG to another
post.
With fwknop now re-written in C for the 2.0 release,
I thought it would be a good idea to take a look at how close encrypted SPA packet data comes to having
high levels of entropy - as understood to be a measure of randomness - from one packet to the next. If
fwknop is properly using encryption, and the ciphers themselves are also well-implemented (fwknop can
use either Rijndael or GPG), then we would expect there to be no obvious relationship between SPA packets
even for repeated access requests to the same service. If there are any such relationships in the
encrypted data across multiple SPA packets, then an adversary might be able to infer things about
the underlying plaintext - precisely what strong encryption is supposed to make difficult. This blog
post covers SPA packet entropy for AES (Rijndael) CBC and ECB encryption modes, and leaves GPG to another
post.
Although this post has some similarities with an older blog entry "Visualizing SPA Packet Randomness", a more rigorous and automated way of measuring cross-packet SPA entropy will be presented. In addition, we'll take a look at what happens when (normally) random salt values for AES encrypted SPA packets are artificially forced to be constant. This helps to highlight some real differences in AES electronic codebook (ECB) and cipher block chaining (CBC) encryption modes.
First, the next release of fwknop will most likely offer the ability to select different AES encryption modes (such as cipher feedback (CFB) mode and output feedback (OFB) mode), and a dedicated "crypto_update" branch has been created for this work. The default AES encryption mode used by fwknop is cipher block chaining (CBC) mode as defined here. Within the crypto_update branch there is a new script "spa-entropy.pl" that is designed to execute the fwknop client multiple times, collect the encrypted SPA packet data, use the ent program to measure the entropy in slices for each byte position across the SPA data set, and then plot the results with gnuplot. What does this accomplish? It allows us to easily see for any given byte position within a collection of SPA packets whether there is a relation from one to the next. If there is such a relation, then the cipher used to encrypt the data was not very good at achieving high levels of entropy in the ciphertext across multiple packets.
As a motivating example from Wikipedia, AES in ECB mode encrypts identical plaintext blocks into identical ciphertext blocks, and this results in patterns in plaintext data being preserved to some extent in the ciphertext. So, an adversary can make good guesses about the underlying plaintext just by looking at the ciphertext! Wikipedia does a nice job of illustrating this with the following two images of the Linux kernel mascot "Tux" - before and after AES encryption in ECB mode:
 |
AES ECB encryption -> |  |
Now, let's take a look at SPA packet entropy with the spa-entropy.pl script. For reference, fwknop builds SPA packets according to the following data format before encryption:
[random data: 16 bytes]:[username]:[timestamp]:[version]:[message type]:[access request]:[digest]
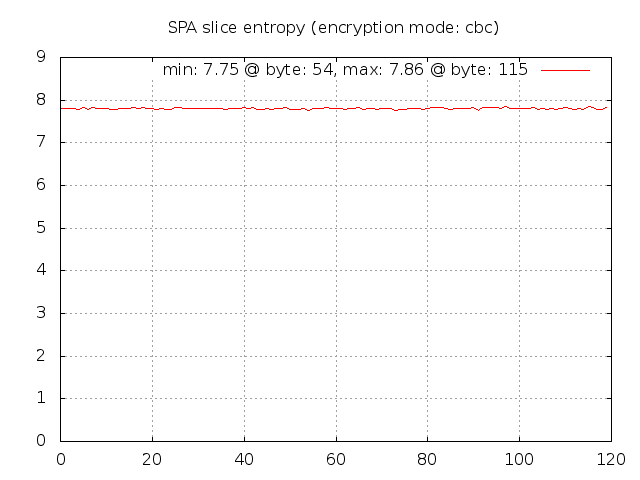
So, if a user wants repeated access to the same service protected behind fwknopd on some system, then several fields above will be identical across the corresponding SPA packets before they are encrypted. The username, version, message type, and access request fields will likely be the same. If fwknop has made proper use of encryption, then the fact that these fields are the same across multiple SPA packets should not matter. After encryption, an observer should not be able to tell anything about the underlying plaintext (other than perhaps size since AES is a block cipher). Let's verify this for 1,000 SPA packets encrypted with the default CBC mode - they are all encrypted with the same key 'fwknoptest' by the spa-entropy.pl script:
$ ./spa-entropy.pl -f 1000_pkts.data -r -c 1000 --base64-decode
[+] Running fwknop client via the following command:
LD_LIBRARY_PATH=../../lib/.libs ../../client/.libs/fwknop -A tcp/22 -a 127.0.0.2 -D 127.0.0.1 --get-key local_spa.key -B 1000_pkts.data -b -v --test -M cbc
[+] Read in 1000 SPA packets...
[+] Min entropy: 7.75 at byte: 54
[+] Max entropy: 7.86 at byte: 115
[+] Creating entropy.gif gnuplot graph...
This produces the gnuplot graph below. Perfectly random data would produce
8 bits of entropy per byte, and the min/max values of 7.75 and 7.86 along with the fairly
uniform distribution of similar values across all of the SPA byte positions implies that
there is little relation from one SPA packet to the next - good.
 As an aside, here is
what ent reports against the local /dev/urandom entropy source on my Linux system, and it is
the "Entropy =" line that spa-entropy.pl parses for each SPA byte slice:
As an aside, here is
what ent reports against the local /dev/urandom entropy source on my Linux system, and it is
the "Entropy =" line that spa-entropy.pl parses for each SPA byte slice:
$ dd if=/dev/urandom count=1000 |ent
1000+0 records in
1000+0 records out
512000 bytes (512 kB) copied, 0.128497 s, 4.0 MB/s
Entropy = 7.999625 bits per byte.
Optimum compression would reduce the size
of this 512000 byte file by 0 percent.
Chi square distribution for 512000 samples is 265.77, and randomly
would exceed this value 50.00 percent of the times.
Arithmetic mean value of data bytes is 127.5076 (127.5 = random).
Monte Carlo value for Pi is 3.138715386 (error 0.09 percent).
Serial correlation coefficient is -0.001293 (totally uncorrelated = 0.0).
Now, let's switch to ECB mode and see what happens (just run the spa-entropy.pl script
with '-e ecb'):
 Well, that still looks pretty good. Revisiting the ECB encrypted image of Tux above
for a moment - the reason that the Tux outline can be seen in the encrypted version
is that in the JPG image file there must be identical blocks in multiple locations
to represent the solid black regions. These blocks are all encrypted in the same
way by AES in ECB mode, so the outline persists. But, this is one instance of ECB
encryption against a file that has multiple identical blocks. For the encrypted SPA
packets, we're dealing with 1,000 separate instances of encrypted data (all with the
same key). Across this data set there are certainly lots of identical plaintext
blocks (all of the SPA packets request access for source IP 127.0.0.2 to destination
port tcp/22 for example), but the encrypted data still shows a high level of entropy.
This source of entropy is provided by the random salt values that are used to
generate the initialization vector and final encryption key for each encrypted SPA
packet. As proof, if we apply the following patch to force the salt to zero for all
SPA packets (of course, one would not want to use this patch in practice):
Well, that still looks pretty good. Revisiting the ECB encrypted image of Tux above
for a moment - the reason that the Tux outline can be seen in the encrypted version
is that in the JPG image file there must be identical blocks in multiple locations
to represent the solid black regions. These blocks are all encrypted in the same
way by AES in ECB mode, so the outline persists. But, this is one instance of ECB
encryption against a file that has multiple identical blocks. For the encrypted SPA
packets, we're dealing with 1,000 separate instances of encrypted data (all with the
same key). Across this data set there are certainly lots of identical plaintext
blocks (all of the SPA packets request access for source IP 127.0.0.2 to destination
port tcp/22 for example), but the encrypted data still shows a high level of entropy.
This source of entropy is provided by the random salt values that are used to
generate the initialization vector and final encryption key for each encrypted SPA
packet. As proof, if we apply the following patch to force the salt to zero for all
SPA packets (of course, one would not want to use this patch in practice):
$ git diff lib/cipher_funcs.c
diff --git a/lib/cipher_funcs.c b/lib/cipher_funcs.c
index 0a0ce3b..32c8bd6 100644
--- a/lib/cipher_funcs.c
+++ b/lib/cipher_funcs.c
@@ -153,6 +153,8 @@ rij_salt_and_iv(RIJNDAEL_context *ctx, const char *pass, const unsigned char *da
get_random_data(ctx->salt, 8);
}
+ memset(ctx->salt, 0x00, 8);
+
/* Now generate the key and initialization vector.
* (again it is the perl Crypt::CBC way, with a touch of
* fwknop).
Here is what spa-entropy.pl reports after recompiling fwknop with the patch above:
 Now we can easily see where there are identical blocks across the SPA packet data set. The first
eight bytes contains the salt, so these are all zero (note that fwknop strips the
usual "Salted__" prefix before transmitting an SPA packet on the wire). The next
16 bytes are the random bytes that fwknop includes in every SPA packet so these bytes
have high entropy. Next up are the username and timestamp - the later changes with
each second, so there is some entropy there since it takes a few seconds to create the
1,000 SPA packet data set. Then the entropy goes back to zero with the next fields
and there isn't any decent entropy until the final message digest.
Now we can easily see where there are identical blocks across the SPA packet data set. The first
eight bytes contains the salt, so these are all zero (note that fwknop strips the
usual "Salted__" prefix before transmitting an SPA packet on the wire). The next
16 bytes are the random bytes that fwknop includes in every SPA packet so these bytes
have high entropy. Next up are the username and timestamp - the later changes with
each second, so there is some entropy there since it takes a few seconds to create the
1,000 SPA packet data set. Then the entropy goes back to zero with the next fields
and there isn't any decent entropy until the final message digest.
As a final contrasting case, let's leave the patch applied to force the salt to zero, but now switch back to CBC mode:
 In CBC mode, the random data included by the fwknop client now results in decent entropy
even though the salt is zero. This is because every ciphertext block in CBC mode
depends on all previous plaintext blocks, so randomness in one plaintext block implies
that every subsequent encrypted block will look different from one SPA packet to the
next. This graphically shows that CBC mode is a better choice for strong security.
Now, if the pseudo random number generator on the local operating system is poorly
implemented, this will negatively impact ciphertext entropy regardless of the encryption
mode, but still CBC mode is a better alternative than ECB mode.
In CBC mode, the random data included by the fwknop client now results in decent entropy
even though the salt is zero. This is because every ciphertext block in CBC mode
depends on all previous plaintext blocks, so randomness in one plaintext block implies
that every subsequent encrypted block will look different from one SPA packet to the
next. This graphically shows that CBC mode is a better choice for strong security.
Now, if the pseudo random number generator on the local operating system is poorly
implemented, this will negatively impact ciphertext entropy regardless of the encryption
mode, but still CBC mode is a better alternative than ECB mode.
Although spa-entropy.pl is geared towards measuring SPA packet entropy, this technique could certainly be generalized to arbitrary collections of ciphertext. If you know of such an implementation, please email me.




