Visualizing SPA Packet Randomness
18 September, 2008
 A key advantage to using Single Packet Authorization (SPA) over
port knocking is the fact that it is trivially easy to harden SPA packets against replay
attacks by including a significant number of random bytes within each SPA packet. Then, by
tracking the SHA-256 message digest (or the digest from some other suitable cryptographic
hashing algorithm) for all incoming SPA packets, the server can enforce that only unique
SPA packets ever result in elevated access through a default-drop firewall policy. Any
duplicate SPA packet will match a previously calculated digest, and such a packet is
therefore flagged as a replay attack (subject to the usual concerns surrounding the
minuscule chance of a hash collision - though for SHA-256 this is exceedingly unlikely).
In the case of SPA packets generated by the fwknop client, a full 16 bytes of
random data is included at the beginning of each packet before it is encrypted.
A key advantage to using Single Packet Authorization (SPA) over
port knocking is the fact that it is trivially easy to harden SPA packets against replay
attacks by including a significant number of random bytes within each SPA packet. Then, by
tracking the SHA-256 message digest (or the digest from some other suitable cryptographic
hashing algorithm) for all incoming SPA packets, the server can enforce that only unique
SPA packets ever result in elevated access through a default-drop firewall policy. Any
duplicate SPA packet will match a previously calculated digest, and such a packet is
therefore flagged as a replay attack (subject to the usual concerns surrounding the
minuscule chance of a hash collision - though for SHA-256 this is exceedingly unlikely).
In the case of SPA packets generated by the fwknop client, a full 16 bytes of
random data is included at the beginning of each packet before it is encrypted.
Another benefit of randomizing SPA packet data - beyond thwarting replay attacks - is that it becomes more difficult to write signatures for intrusion detection systems to detect SPA traffic. The structure of SPA packets generated by the fwknop client is designed to minimize sections that remain the same from one invocation of the client to the next - such identifying sections could be used to write Snort rules to detect fwknop SPA packets. This blog post contains examples of such Snort rules which look for the base64-encoded versions of the string "Salted__" or the hex bytes "0x8502" at the very beginning of UDP packets over port 62201 (the default port used by fwknop). There is also a rule to look for trailing '=' characters at the end of such packets in order to detect the marker used by base64 encoding when the length of the original data is not a multiple of four. These predictable bytes are artifacts of the Crypt::CBC module, GnuPG, or base64 encoding itself, but any recent release of fwknop strips these bytes out of SPA packets before sending them on the wire. The fwknopd server adds them back in if necessary before attempting to base64 decode and decrypt incoming SPA packets.
So, given that fwknop uses CBC mode for symmetric encryption and random bytes are at the very beginning of the payload data, one would expect that SPA packets from fwknop - when viewed via a sniffer - are essentially random variations of base64-encoded data, correct? And this should remain true across all SPA packets that are encrypted with the same encryption key, and even across the same access requests?
Let's see how close fwknop gets to this...
What we need to see is the distribution of byte values across each byte position in a large sampling of SPA packets. That is, for the first byte in each packet across our sample, can we find a relation to any of the other first bytes in the other packets? This process needs to be repeated across all bytes in every packet. To rigorously test for randomness properties we could also get more sophisticated and use the NIST Statistical Test Suite, but for now we'll just focus on using Gnuplot to visualize the byte distribution across two sets of 20,000 SPA packets. If Gnuplot shows any recognizable features or relationships across our sample sets, then we know that we have more work to do. For reference, if you want to duplicate the analysis in this blog post or perform your own analysis of the SPA packet data sets (20,000 packets each), you can download them.
We need two capabilities: 1) the ability to automatically generate 20,000 SPA packets with the fwknop client and store them in a file (one packet to a line), and 2) the ability to parse the file and count the number of different characters in each byte position across all 20,000 SPA packets and print this data to a file so that it can be graphed. These goals are accomplished with this patch to fwknop (which adds a new command line argument --Save-packet-append to be released in fwknop-1.9.8) and this script base64_byte_frequency.pl respectively.
Now, let's collect the first set of 20,000 SPA packets. Each packet is encrypted in this case with the Rijndael cipher, and we use the --Include-salted and --Include-equals command line arguments to produce SPA packets that are compatible with older fwknopd servers:
[spaclient]$ for ((i=1;i<=20000;i+=1)); do fwknop -A tcp/22
-a 127.0.0.1 -D 127.0.0.1 --Save-packet --Save-packet-file
spa_artifacts.pkts --Save-packet-append --get-key spa.pw
--Include-salted --Include-equals > /dev/null; echo $i; done
1
2
3
...
19998
19999
20000
[spaclient]$ head -n 2 spa_artifacts.pkts
U2FsdGVkX1/s7OmvQtYk9UnQuGg8htJ+19pru9NdhflmGhS9d/9fFET7jnPKWsk3/lnd
CbGprkkUBkEYXNORP8RU8ZhkCS+pexZ2J+FbQzmwiuD7/9nA1DAmBGnUQi7mLyZYtOGm
iCa8yL9IaP43DVhMflAEf+tQGaPw5xUd2/0=
U2FsdGVkX18NuTMq50ef6hjD0t16ZUnKrVYjirVW81UIRNDfclS812vZAWTdcio8t3GC
QVxZz/uwrJsjkzevD0OhxJhba+CQVeKuJpfUOhskDQMtYDcH2hkGeDRK9Oc6AfLjO5Fd
JXxBJuf8pmxfLC2iWkfAfooCJpjkOm+afH4=
All of the SPA packets generated by the command above are written to the file spa_artifacts.pkts,
and now let's execute the base64_byte_frequency.pl script against it. This
script will create two new files spa_artifacts.pkts.2d and spa_artifacts.pkts.3d
for graphing in two and three dimensions. The 2D file contains a simple count of each
base64 encoded character, and the 3D file contains a count of each character at each
position in the collection of SPA packets. We'll use Gnuplot to graph this data as
follows:
[spaclient]$ ./base64_byte_frequency.pl spa_artifacts.pkts
[+] Parsing SPA packets from: spa_artifacts.pkts...
[+] Writing 2D results to: spa_artifacts.pkts.2d...
[+] Writing 3D results to: spa_artifacts.pkts.3d...
[spaclient]$ cat > spa_artifacts_2d.gnu
reset
set title "2D SPA packet randomness (artifacts included)"
set terminal png transparent nocrop enhanced
set output "spa_artifacts_2d.png"
set xlabel "char"
set ylabel "frequency"
plot 'spa_artifacts.pkts.2d' using 1:2 with lines title '(char,freq)'
[spaclient]$ cat > spa_artifacts_3d.gnu
reset
set title "3D SPA packet randomness (artifacts included)"
set terminal png transparent nocrop enhanced
set output "spa_artifacts_3d.png"
set xlabel "position"
set ylabel "char"
set zlabel "frequency"
set view 72,9
splot 'spa_artifacts.pkts.3d' using 1:2:3 with points title '(pos,char,freq)'
[spaclient]$ gnuplot spa_artifacts_3d.gnu
[spaclient]$ gnuplot spa_artifacts_2d.gnu
[spaclient]$ ls -atlr *png
-rw-r--r-- 1 mbr mbr 5977 2008-09-14 09:31 spa_artifacts_2d.png
-rw-r--r-- 1 mbr mbr 4194 2008-09-14 09:31 spa_artifacts_3d.png
The last two lines above indicate that Gnuplot has created two graphics files
spa_artifacts_2d.png and spa_artifacts_3d.png for plotting the data
in two and three dimensions. Because we're graphing base64 characters as integer data,
the base64_byte_frequency.pl script maps each base64 character to numerically
ordered values beginning at zero. We could have just graphed the hex value of each
character directly, but this would result in gaps. For reference, the base64 alphabet
is described by the following characters (in order): +, /, 0-9, A-Z, a-z. There is
also the equals "=" character, but it is only used as a closing marker. So, the
base64_byte_frequency.pl script maps "+" to 0, "/" to 1, "0-9" to 1-11, "A-Z"
to 12-37, "a-z" to 38-63, and "=" to 64.
Here is the 2-dimensional graph that Gnuplot has produced:
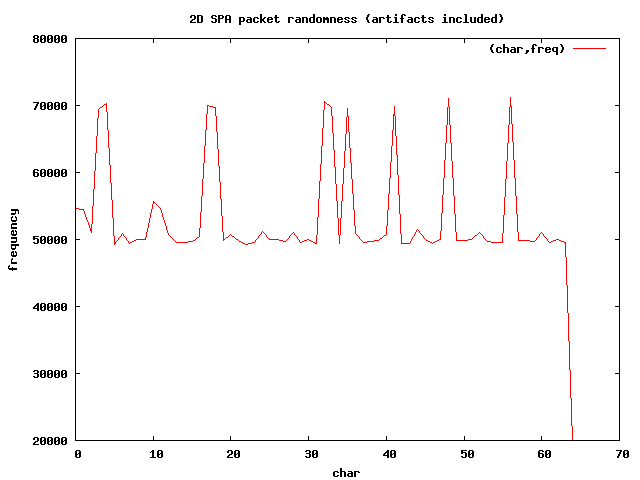 You can see in the graph above that there are several spikes for a few character values.
These spikes correspond with the characters U2FsdGVkX1, which is the base64
encoded version of the string "Salted__". Every SPA packet in the spa_artifacts.pkts
file begins with this string, and so one would expect more of these characters on
average than the others. There is also a sharp dip to 20,000 on the right-hand
portion of the graph for the value 64, which corresponds to the = character.
This is because there is only one equals character at the end of each SPA packet in
the spa_artifacts.pkts file.
You can see in the graph above that there are several spikes for a few character values.
These spikes correspond with the characters U2FsdGVkX1, which is the base64
encoded version of the string "Salted__". Every SPA packet in the spa_artifacts.pkts
file begins with this string, and so one would expect more of these characters on
average than the others. There is also a sharp dip to 20,000 on the right-hand
portion of the graph for the value 64, which corresponds to the = character.
This is because there is only one equals character at the end of each SPA packet in
the spa_artifacts.pkts file.
Because base64 encoding uses an alphabet of 64 characters, and given that our sample size is 20,000 packets of 171 bytes each (less the ending = marker), we would expect the average number of times each character is represented to be 171 / 64 * 20000 = 53,000 (approximately). That is, we can expect this value if the SPA packets are perfectly random across the sample set. The spikes in the 2D graph throw this expected value off a bit.
Now let's take a look at the 3-dimensional plot of the same data:
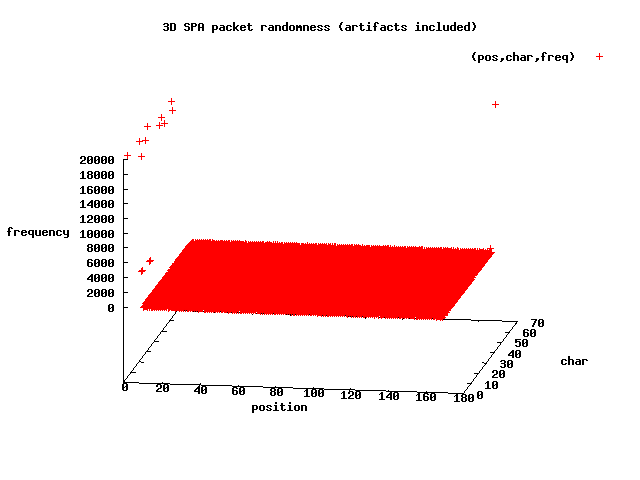 This graph shows us where the predictable bytes are. We know that each SPA
packet begins with U2FsdGVkX1 and ends with =, and the outliers (on the
left-hand side and one point on the right-hand side - all with Z-axis values of
about 20,000) in the above graph illustrate this. The X-axis represents the byte
positions of each packet, the Y-axis are the numeric character codes, and the
Z-axis is the number of times a character is counted.
This graph shows us where the predictable bytes are. We know that each SPA
packet begins with U2FsdGVkX1 and ends with =, and the outliers (on the
left-hand side and one point on the right-hand side - all with Z-axis values of
about 20,000) in the above graph illustrate this. The X-axis represents the byte
positions of each packet, the Y-axis are the numeric character codes, and the
Z-axis is the number of times a character is counted.
So, given that any recent release of fwknop removes the "Salted__" prefix and any trailing "=" characters, are the graphs of such SPA packets now highly randomized?
The answer is "almost".
Let's produce the same two graphs, but this time for SPA packets produced by any recent version of fwknop (without using the --Include-salted or --Include-equals command line arguments).
[spaclient]$ for ((i=1;i<=20000;i+=1)); do fwknop -A tcp/22
-a 127.0.0.1 -D 127.0.0.1 --Save-packet --Save-packet-file
spa_no_artifacts.pkts --Save-packet-append
--get-key spa.pw > /dev/null; echo $i; done
1
2
3
...
19998
19999
20000
[spaclient]$ head -n 2 spa_no_artifacts.pkts
/ZlXox6SyQsyMpKVj+cxHlmSpMWOaAyxmou5LgThZ58yXlxFrR7BGtqSRJJTELrUgJ2/
RiX9If+NLXEANJSu9nogO8ZG2R6cllQlhT1vM6YiLsktujuV3a7r81I1JSCwC4YZdNQC
Y2xwcRGLMEEhykGhp0RKEYlSo
8jX5NECzw4NGVg3LIEhu30ph0uvBa4ijW9/S7IQEQvdj/IPHle8KRoeyHvskj1fd0XU7
beUIb5zCKsFq7NTTUsnwaccULAKQHZz4Qm0ZTVC8st0doDfhU5Bl46LbDXPCejRbSQEd
cVgwDwaU8XqEKr8kYjXZ3ZNGA
The 2-dimensional graph looks pretty good:
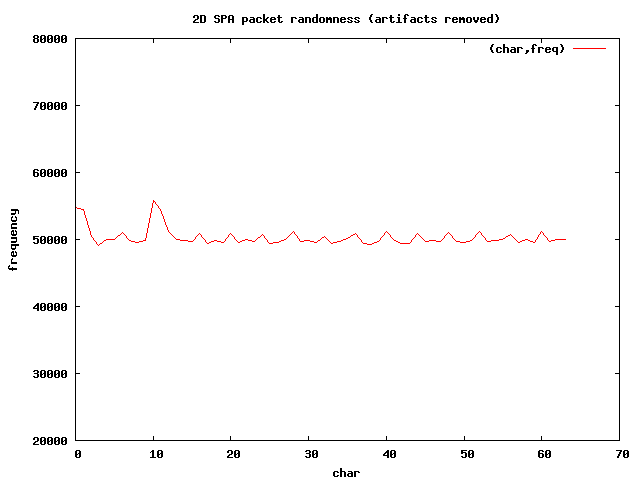 Now that the invariant sections have been removed, the length of each packet is
161 characters, so if the randomness were perfect, we would expect the average
instance of each character to be 161 / 64 * 20000 = 50,300 (approximately), and
this is quite close to the value displayed by the graph.
There are still two minor spikes corresponding to the numeric values around 0
and 1, and then again around 10 and 11 on the X-axis. These bytes correspond to
the characters +, /, 8, and 9 respectively.
Now that the invariant sections have been removed, the length of each packet is
161 characters, so if the randomness were perfect, we would expect the average
instance of each character to be 161 / 64 * 20000 = 50,300 (approximately), and
this is quite close to the value displayed by the graph.
There are still two minor spikes corresponding to the numeric values around 0
and 1, and then again around 10 and 11 on the X-axis. These bytes correspond to
the characters +, /, 8, and 9 respectively.
Let's look at the 3-dimensional graph to see if we can get a sense of where these spikes are in terms of byte positions within the SPA packets:
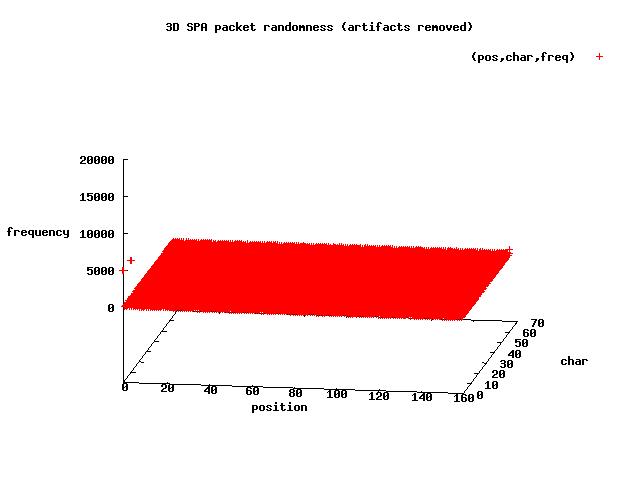 So, at the scale shown above, the 3D graph looks decently random - at least there
are far fewer outliers than for the first data set of 20,000 packets, and there aren't
any other obviously regular structures in the graph. However, if you look to the
left-hand portion of the graph, you will see there are
small outliers at position 0 on the X-axis - the very first byte of each SPA
packet. Looking through the spa_no_artifacts.pkts file, the graph is indeed
correct - every SPA packet begins with one of the bytes +, /, 8, or 9.
So, at the scale shown above, the 3D graph looks decently random - at least there
are far fewer outliers than for the first data set of 20,000 packets, and there aren't
any other obviously regular structures in the graph. However, if you look to the
left-hand portion of the graph, you will see there are
small outliers at position 0 on the X-axis - the very first byte of each SPA
packet. Looking through the spa_no_artifacts.pkts file, the graph is indeed
correct - every SPA packet begins with one of the bytes +, /, 8, or 9.
Why?
The reason is that the current fwknop client code strips the string U2FsdGVkX1 from each SPA packet after the raw encrypted data is base64 encoded, and the encoding itself uses +, /, 8, or 9 after the last "_" in the string "Salted__". Although this is not huge problem, it does mean that it is possible to write a Snort rule that uses a PCRE to look for one of these bytes at the very beginning of UDP payload data. This will be fixed in a future release of fwknop.
The techniques illustrated in this blog post can be applied to SPA packets generated by other implementations as well. Some SPA implementations use a hashed payload instead of an encrypted payload which implies that multiple requests for the same access through a firewall will look quite similar in many byte positions, so it is much easier to detect such SPA packets with signatures in an intrusion detection system. By contrast, the SPA packets produced by fwknop are much harder to write reliable signatures for effective detection in any IDS - particularly when combined with the port randomization features offered in recent releases.
Finally, this blog post has only addressed the randomness characteristics of SPA packets that have been encrypted with the Rijndael cipher. An upcoming blog post will perform the same analysis for SPA packets encrypted with GnuPG.




